3 O projeto Sol-Terra-Lua
Neste capítulo, aprenderemos o uso básico do A-Frame por meio do desenvolvimento de um projeto para ensino de Astronomia.
No projeto Sol-Terra-Lua (abrev. STL) iremos:
- Criar as esferas solar, terrestre e lunar no espaço tridimensional em realidade aumentada.
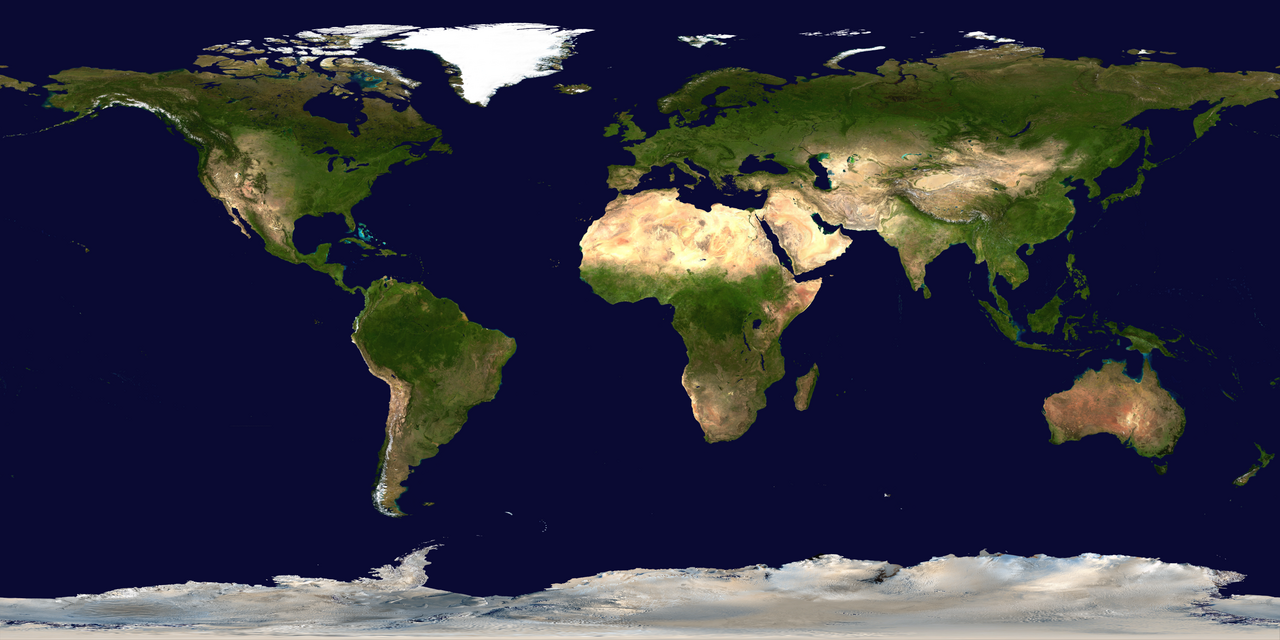
- Texturizar a superfície das esferas com os mapas dos respectivos astros.
- Estabelecer os tamanhos e posições dos astros de forma pertinente aos objetivos didáticos de uma atividade educacional.
- Implementar o movimento de rotação de cada astro em torno do próprio eixo.
- Definir o plano orbital da Terra e da Lua.
- Implementar o movimento orbital de translação da Terra e da Lua.
- Dar interatividade aos objetos celestes.
3.1 Elementos HTML do A-Frame
Todo o desenvolvimento do projeto será realizado no Glitch. Vide Seção 2.3.
- Faça o login na sua conta do Glitch e remixe o projeto aframe-minicurso-vr
Repare que o projeto está bastante vazio, com apenas o arquivo index.html e sem qualquer código Javascript explícito. Entretanto, temos dentro do head a inclusão do arquivo online:
https://aframe.io/releases/1.6.0/aframe.min.js.
É esse arquivo, acessado remotamente, que disponibilizará o núcleo de funcionalidades do A-Frame.
- O elemento HTML básico e obrigatório do A-Frame é o
a-scene(Cena), o qual temos que incluir dentro do elementobodyconforme o Código 3.1.
<body>
<a-scene>
</a-scene>
</body>a-scene, de uma página HTML com A-Frame.
Dentro do a-scene todos os elementos espaciais do projeto serão incluídos. Esses elementos recebem o nome de a-entity (Entidades). Cada entidade, por sua vez, terá uma série de propriedades, chamadas de components (Componentes). Por fim, cada componente terá atributos que definirão as aparências e funcionalidades da entidade.
Esse tipo de estruturação segue o modelo ECS (Entity-Component-System) que é alternativo ao modelo de classes e objetos. Ele se opõe ao sistema de hierarquização da programação orientada a objetos ao permitir maior modularização e inter-operacionalização dos componentes que podem ser aplicados diretamente em diferentes entidades.
De forma abstrata, uma estrutura ECS no A-Frame poderia ser algo assim:
Cena:
Entidade 1:
- Componente A -> Atributo A1: valor E1A1; Atributo A2: valor E1A2
- Componente B -> Atributo B1: valor E1B1; Atributo B2: valor E1B2
Entidade 2:
- Componente A -> Atributo A1: valor E2A1; Atributo A2: valor E2A2
- Componente C -> Atributo C1: valor E2C1; Atributo C2: valor E2C2
Um exemplo mais concreto seria:
a-scene:
a-entity
id = "carro":rodas = "quantidade : 4; aro: 20"material = "cor: azul; metalicidade: 0.5"
a-entity
id = "moto":rodas = "quantidade : 2; aro: 40"material = "cor: vermelho; metalicidade: 0.8"

Nesse exemplo, carro e moto são entidades distintas, mas rodas e material são componentes que podem ser usados pelas diferentes entidades. Esses componentes irão se diferenciar por possuírem valores diferentes para os seus atributos (e.g. rodas com quantidade : 2 ou quantidade : 4) e por estarem atrelados a diferentes entidades. Uma das vantages dessa abordagem ECS é que eu preciso programar o componente rodas somente uma vez e ele pode ser usado em diferentes veículos.
Entidades podem ser aninhadas. Por exemplo, ao invés de tratar as rodas como sendo componentes, poderíamos considerar mais apropriado implementá-las na forma de uma entidade:
a-scene:
a-entity
id = "fusca":a-entity
id = "rodas_do_fusca":material = "cor: preto; metalicidade: 0.1"dimensoes = "aro: 20; largura: 10; quantidade: 4"
a-entity
id = "moto":rodas = "quantidade : 2; aro: 40"material = "cor: vermelho; metalicidade: 0.8"
Vamos então criar nossa primeira entidade: o planeta Terra.
- Coloque a entidade do Código 3.2 dentro do elemento a-scene do Código 3.1.
<a-entity id="terra"
geometry="primitive: sphere"
material="color: blue">
</a-entity>Se fizermos o preview da cena no Glitch poderemos observar a esfera de diferentes ângulos usando o mouse. Mas não conseguiremos dar zoom ou deslocamentos laterais na imagem. Isso ocorre pois não estamos usando os óculos de realidade virtual. A melhor forma de interagir com a página gerada na tela do computador, sem os óculos, é escolhendo a opção Preview in a new window no Glitch. Na página que foi aberta, devemos entrar no modo de inspeção (Visual inspector) ao digitar a combinação de teclas <ctrl> + <alt> + i.
Nesse modo, cada botão do mouse, quando mantido apertado, permite rotacionar, transladar e aproximar/afastar a visão da cena. Ao clicar em uma entidade é possível também aferir e alterar os valores dos seus atributos. É possível até mesmo criar entidades novas e atribuir componentes no Visual inspector. Ao apertar a tecla h (help), temos acesso a todas as teclas de atalho.
Voltando à Terra, vamos “dar um talento” em nosso pale blue dot.1 Para isso, usaremos uma imagem planificada da superfície da Terra para projetá-la na esfera. Por sorte, o A-Frame faz isso muito diretamente para a gente. Vejamos como.
3.2 Carregando arquivos externos em nosso projeto STL
O A-Frame possui um elemento chamado a-asset para pré-carregar todos os recursos (imagens, áudios, vídeos, etc) que sejam usados na página. Existem duas formas para fazer isso:
- Carregando o recurso dentro do Glitch via Files no menu lateral de arquivos.
- Indicando o endereço de internet (URL) do recurso caso ele esteja disponível.
Neste minicurso, vamos usar somente a segunda opção.
- Clique com o botão direito do mouse sobre o mapa da Terra abaixo e copie o seu link.
- Dentro do elemento
a-sceneinclua o elementoimgconform e o Código 3.3.
<a-assets>
<img id="mapa_terra" src="substitua_isto_pelo_endereço_da_imagem">
</a-assets>a-asset.
- Em seguida substitua o atributo color por src no componente material da entidade
terra, usando como valor aiddo mapa da Terra, resultando no Código 3.4
<a-entity id="terra"
geometry="primitive: sphere"
material="src: #mapa_terra">
</a-entity>terracom atributo src no lugar de color.
Além do Visual Inspector, o A-Frame possui um componente para navegação mais facilitada na cena quando não estamos usando os óculos de Realidade Virtual. Para incluí-lo no projeto basta incluir o script abaixo dentro element head:
<script src="https://unpkg.com/aframe-orbit-controls@1.3.2/dist/aframe-orbit-controls.min.js"></script>E incluir a seguinte a-entity de câmera dentro do elemento a-scene:
<a-entity camera look-controls="enabled: false" orbit-controls="target: 0 0 0; minDistance: 0; maxDistance: 180; initialPosition: 0 3 5; rotateSpeed: 1.5"></a-entity>3.3 Sistemas de coordenadas no A-Frame
Um conceito fácil de implementar no A-Frame são os sistemas de coordenadas locais (também chamados de referenciais), que são produzidos quando você aninha uma a-entity dentro de outra.
Pense que cada entidade tem seu próprio sistema de coordenadas (x, y, z), que define sua posição, rotação e escala. Quando uma a-entity está dentro de outra, dizemos que a entidade interna usa o sistema de referência local da entidade que a contém. Isso significa que qualquer transformação (movimento, rotação) aplicada à entidade “pai” afeta todas as suas “filhas” de forma relativa. Ou seja, quando criamos uma a-entity, não definimos apenas as propriedades do objeto 3D pelas suas componentes, mas também, implicitamente, criamos um sistema de coordenadas local.
Podemos, ainda, criar uma a-entity sem componentes geométricos ou atributos. Nesse caso, ela serve exclusivamente como um sistema de coordenadas de referência para todas as outras entidades que sejam aninhadas dentro dela.
E o nosso projeto Sol-Terra-Lua se beneficia diretamente desse recurso. Vamos considerar uma a-entity que representa, exclusivamente, o referencial Terra (ref_terra) e dentro dela outra a-entity que representa a Lua. Se você mover ou rotacionar o referencial Terra (a entidade “pai”), a Lua (a entidade “filha”) será movida junto, mas ela ainda pode orbitar ao redor do referencial Terra se aplicarmos uma rotação à Lua individualmente. Assim, a Lua se move de duas maneiras: ela orbita o Sol ao “seguir” a Terra (movimento da entidade “pai”) e orbita a Terra (movimento da entidade “filha”).2 O Vídeo 3.1 ilustra esse conceito.
a-entity ref-Terra (referencial “pai”), a a-entity lua (entidade filha) desloca-se conjuntamente. Ao deslocar a a-entity lua, a a-entity ref_Terra permanece inalterada.
Portanto, o A-Frame é muito prático para simular cenários em que o movimento de um objeto depende de outro, como no caso de planetas em órbita, satélites, ou até objetos conectados em uma cadeia de eventos. Ao invés de ter que recalcular constantemente as posições de todos os objetos manualmente, o A-Frame faz isso automaticamente ao respeitar as hierarquias de aninhamento.
3.4 Cada astro em seu lugar
Neste ponto, temos todos os elementos para a construção do sistema Sol-Terra-Lua.
- Primeiramente, vamos atualizar os nossos assets com as imagens das superfícies do Sol e da Lua conforme o Código 3.5.
<a-assets>
<img id="mapa_sol" src="https://upload.wikimedia.org/wikipedia/commons/thumb/9/99/Map_of_the_full_sun.jpg/1280px-Map_of_the_full_sun.jpg">
<img id="mapa_terra" src="https://upload.wikimedia.org/wikipedia/commons/thumb/2/23/Blue_Marble_2002.png/1280px-Blue_Marble_2002.png">
<img id="mapa_lua" src="https://upload.wikimedia.org/wikipedia/commons/thumb/d/d1/Solarsystemscope_texture_8k_moon.jpg/1280px-Solarsystemscope_texture_8k_moon.jpg">
</a-assets>Vamos agora inserir cada astro em seu devido lugar e com o seu devido tamanho. Poderíamos respeitar a escala relativa de tamanhos, mas como o Sol é muito maior que a Terra (cerca de 100 vezes), vamos adotar uma escala alternativa para fins didáticos. O mesmo vale para as distâncias entre os astros (a distância Sol-Terra é quae 400 vezes maior que a Terra-Lua).
A Tabela 3.1 contém os tamanhos (raios esféricos) e distâncias ao astro “pai” (raios orbitais) dos astros do projeto.
| Astro | Raio esférico | Raio orbital |
|---|---|---|
| Sol |
|
|
| Terra |
|
|
| Lua |
|
|
Vamos criar o sistema de coordenadas de cada astro a uma distância do astro “pai” igual aos raios orbitais (util) da Tabela 3.1. O Sol será a entidade que comporá o sistema de coordenadas pai. Dentro dele, criaremos uma entidade para o referencial Terra e, dentro deste, o referencial Lua.
Teremos, portanto, o seguinte aninhamento de sistemas de coordenadas:
<a-entity id="pos_sol" position="0 0 0">
<a-entity id="pos_terra" position="1.5 0 0">
<a-entity id="pos_lua" position="0 0 0.5">
</a-entity>
</a-entity>
</a-entity>Repare que para as distâncias usamos o componente position cujo atributo é uma trinca de coordenadas x, y, z.
Agora, vamos colocar a entidade que representa a esfera de cada astro dentro dos respectivos referenciais. Para isso, substitua o Código 3.4 pelo Código 3.6.
<a-entity id="pos_sol" position="0 0 0">
<a-entity id="sol"
geometry="primitive: sphere; radius: 0.3"
material="src: #mapa_sol">
</a-entity>
<a-entity id="pos_terra" position="1.5 0.0 0">
<a-entity id="terra"
geometry="primitive: sphere; radius: 0.15"
material="src: #mapa_terra">
</a-entity>
<a-entity id="pos_lua" position="0 0.0 0.5">
<a-entity id="lua"
geometry="primitive: sphere; radius: 0.05"
material="src: #mapa_lua">
</a-entity>
</a-entity>
</a-entity>
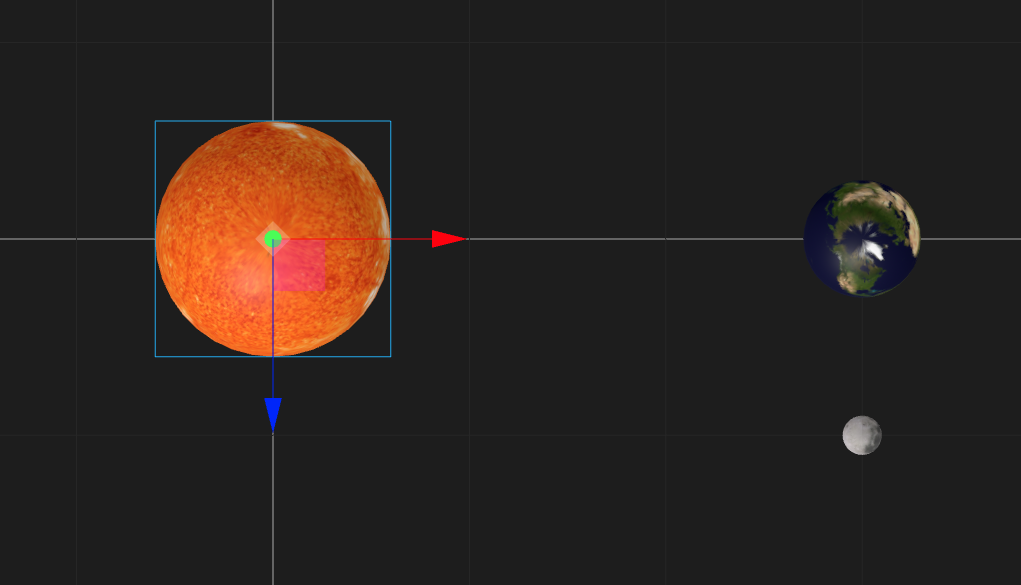
</a-entity>Repare que para o raio esférico de cada astro usamos o atributo radius do componente geometry. Outra observação é que todas as dimensões são informadas ao A-Frame sem explicitar as unidades, pois o A-Frame considera todas elas em metros por padrão. A Figura 3.2 mostra a disposição geométrica do sistema.
3.5 Animando as coisas
Como diria o sábio Galileu, “Eppur si muove”.3 Vamos então pôr o mundo a girar.
O A-Frame possui várias possibilidades de animação built in através do componente animation. Os atributos principais desse componente são:
property: a propriedade da entidade que será animada, e.g. ângulo de rotação, posição, grau de transparência, etc.from: o valor inicial da propriedade (default: o valor atual).to: o valor final da propriedade ao término da animação.dur: duração da animação em milissegundos.loop: se a animação deve ser reiniciada automaticamente (trueoufalse).easing: a taxa de variação da propriedade (default: aumento quadrático = aceleração constante).dir: sentido da animação (normaloureverse).
3.5.1 Movimento orbital
O movimento orbital, também conhecido por movimento de translação, será implementado por uma entidade específica (e.g. orb_terra) colocada acima da entidade do raio orbital (e.g. pos_terra). Essa entidade terá o componente animation que rotacionará a a-entity pos_terra que por sua vez está deslocada do centro pelo raio orbital especificado na componente position.
Da mesma forma que fizemos com as dimensões espaciais, não seremos fieis às proporções temporais da dinâmica dos astros. A Tabela 3.2 contém os períodos de rotação e orbital que escolhemos para os três astros.
| Astro | Período de rotação | Período orbital |
|---|---|---|
| Sol |
|
|
| Terra |
|
|
| Lua |
|
|
Por exemplo, considerando somente o movimento orbital da Terra, teríamos o seguinte código:
<a-entity id="orb_terra" animation="property: rotation; to: 0 360 0; loop: true; dur: 300000; easing: linear">
<a-entity id="pos_terra" position="1.5 0.0 0">
<a-entity id="terra"
geometry="primitive: sphere; radius: 0.15"
material="src: #mapa_terra">
</a-entity>
</a-entity>
</a-entity>Com ele, deveremos observar a Terra orbitando em torno do Sol ad aeternum (loop: true) com velocidade constante (easing: linear) e executando uma revolução (to: 0 360 0) a cada 300 segundos (dur: 300000) conforme Vídeo 3.2.
animation da a-entity orb_terra. A cada órbita completa a Terra dá, também, uma volta em torno do próprio eixo (quando próxima à câmera apresenta a África voltada para nós, quando longe apresenta o Pacífico). (10x faster)
Com isso, conseguimos implementar o movimento orbital da Terra. Entretanto, essa animation produz, adicionalmente, um movimento de rotação da Terra em torno do próprio eixo. Esse é um efeito indesejado, pois queremos que o movimento de rotação e o orbital sejam independentes um do outro.
Se quisermos implementar corretamente a rotação da Terra e da Lua em torno de um eixo fixo, temos que compensar essa rotação espúria. Caso contrário, a direção do eixo ficará girando em torno da perpendicular à órbita em um movimento conhecido como precessão.4
Para reverter essa rotação indesejada, podemos utilizar uma animation de rotação no sentido contrário dir: reverse em uma nova entidade a-entity rev_rot_terra dentro da a-entity pos_terra. Ficando da seguinte forma:
<a-entity id="orb_terra" animation="property: rotation; to: 0 360 0; loop: true; dur: 300000; easing: linear">
<a-entity id="pos_terra" position="1.5 0.0 0">
<a-entity id="rev_rot_terra" animation="property: rotation; to: 0 360 0; loop: true; dur: 300000; easing: linear; dir: reverse">
<a-entity id="terra"
geometry="primitive: sphere; radius: 0.15"
material="src: #mapa_terra">
</a-entity>
</a-entity>
</a-entity>
</a-entity>Esse código resulta no movimento orbital da Terra sem o movimento espúrio de rotação em torno do próprio eixo, conforme vemos no Vídeo 3.3.
animation com rotação no sentido contrário dir:reverse. Nesse caso, a Terra não gira em torno do próprio eixo, estando as Américas sempre voltadas para a câmera. (10x faster)
3.5.2 Movimento de rotação
Agora vamos implementar o movimento desejado de rotação da Terra em torno do próprio eixo.
Fazemos isso incluindo o componente animation na a-entity terra:
<a-entity id="terra"
geometry="primitive: sphere"
material="src: #mapa_terra"
1 animation="property: rotation; to: 0 360 0; loop: true; dur: 10000; easing: linear">
</a-entity>- 1
-
Componente
animationpara rotação da Terra.
Assim, deveremos observar a Terra girando ad aeternum (loop: true) com velocidade constante (easing: linear) e executando uma revolução (to: 0 360 0) a cada 10 segundos (dur: 10000). O Vídeo 3.4 mostra esse movimento isoladamente (sem o movimento orbital).
animation.
3.5.3 Movimento completo
- Implementado os movimentos de rotação e orbital discutidos acima no sistema Sol-Terra-Lua completo temos o Código 3.7 que substitui o Código 3.6
<a-entity id="pos_sol" position="0 0 0">
<a-entity id="sol"
geometry="primitive: sphere; radius: 0.3"
material="src: #mapa_sol"
animation="property: rotation; to: 0 360 0; loop: true; dur: 50000; easing: linear">
</a-entity>
<a-entity id="orb_terra" animation="property: rotation; to: 0 360 0; loop: true; dur: 300000; easing: linear">
<a-entity id="pos_terra" position="1.5 0.0 0">
<a-entity id="rev_rot_terra" animation="property: rotation; to: 0 360 0; loop: true; dur: 300000; easing: linear; dir: reverse">
<a-entity id="terra"
geometry="primitive: sphere; radius: 0.15"
material="src: #mapa_terra"
animation="property: rotation; to: 0 360 0; loop: true; dur: 10000; easing: linear">
</a-entity>
<a-entity id="orb_lua" animation="property: rotation; to: 0 360 0; loop: true; dur: 30000; easing: linear">
<a-entity id="pos_lua" position="0 0.0 0.5">
<a-entity id="lua"
geometry="primitive: sphere; radius: 0.05"
material="src: #mapa_lua">
</a-entity>
</a-entity>
</a-entity>
</a-entity>
</a-entity>
</a-entity>
</a-entity>Há algo importante a observar no código acima. Não implementamos a a-entity rev_lua relacionada à compensação da rotação espúria causada pelo movimento orbital da Lua e nem o animation de rotação da Lua em torno do próprio eixo na a-entity lua. Sabemos que devido ao efeito de “travamento gravitacional” produzido pelas forças de maré atuando ao longo de milhões de anos, a Lua orbita com a mesma face voltada para a Terra. Isso implica que o período de translação coincide com o de rotação. Portanto, nesse caso, a rotação espúria da a-entity orb_lua já nos fornece, de brinde, a rotação da Lua em torno do próprio eixo.
Ao entrar no modo de inspeção (<ctrl><alt>i), a Terra ainda estará parada. Isso ocorre pois devemos acionar o botão ▶ (resume scene) no canto superior esquerdo.
3.6 Refinando o sistema
Se quisermos explorar conceitos como estações do ano, fases da Lua e eclipses, existem certos detalhes do movimento dos astros que podemos abrir mão, como a excentricidade das órbitas, o movimento em torno do centro de massa, movimento de precessão e nutação, entre outros. Mas alguns são essenciais para aqueles fenômenos. São eles:
- a inclinação do eixo de rotação da Terra e
- a inclinação do plano da órbita da Lua.
3.6.1 Inclinação do eixo de rotação da Terra
Como sabemos, o eixo de rotação da Terra possui uma inclinação de 23,4° em relação à direção perpendicular ao plano da órbita. Em nosso sistema, podemos implementar essa inclinação em uma nova a-entity inc_terra colocada imediatamente acima da a-entity terra, usando o componente rotation:
<a-entity id="inc_terra" rotation="23.4 0 0">
<a-entity id="terra"
geometry="primitive: sphere; radius: 0.15"
material="src: #mapa_terra"
animation="property: rotation; to: 0 360 0; loop: true; dur: 10000; easing: linear">
</a-entity>
</a-entity> Repare que a rotação se dá na direção \(x\), uma vez que a perpendicular da órbita está na direção \(y\).
3.6.2 Inclinação do plano orbital da Lua
O plano da órbita da Lua em torno da Terra possui uma inclinação de 5,14° em relação ao plano da órbita da Terra em torno do Sol.5 Apesar de não ser uma inclinação tão alta, é ela que faz com que não tenhamos um eclipse em cada lua nova (Lua entre o Sol e a Terra) ou em cada lua cheia (Terra entre o Sol e a Lua) – ou seja, um eclipse solar e outro lunar todo mês.
Como não estamos utilizando uma escala de tamanhos e distâncias proporcionais ao tamanho real dos astros, precisamos usar uma inclinação maior para reproduzir, aproximadamente, efeito dos eclipses em nosso sistema. Adotaremos uma inclinação de 25°. Faremos isso aplicando o componente rotation na nova entidade a-entity inc_orb_lua imediatamente acima da a-entity orb_lua, conforme o código a seguir.
<a-entity id="inc_orb_lua" rotation="-25 0 0">
<a-entity id="orb_lua" animation="property: rotation; to: 0 360 0; loop: true; dur: 30000; easing: linear">
<a-entity id="rev_orb_lua" animation="property: rotation; to: 0 360 0; loop: true; dur: 30000; easing: linear; dir: reverse">
<a-entity id="pos_lua" position="0 0.0 0.5">
<a-entity id="lua"
geometry="primitive: sphere; radius: 0.05"
material="src: #mapa_lua">
</a-entity>
</a-entity>
</a-entity>
</a-entity>
</a-entity> 3.6.3 The dark side of the Moon
Embora não implique em qualquer efeito prático importante, orientar a Lua com a face correta voltada para a Terra é uma questão simples de resolver e dá mais realismo ao sistema. Verificamos que uma simples rotação de 90° na a-entity lua resolve a questão:
<a-entity id="lua"
geometry="primitive: sphere; radius: 0.05"
material="src: #mapa_lua"
rotation="0 90 0">
</a-entity>Com isso temos todos os movimentos desejados para as nossas finalidades didáticas conforme mostrado no Vídeo 3.6.
3.7 Fiat lux
Para finalizar o sistema STL, precisamos iluminar corretamente a cena. Primeiramente, precisamos que a fonte de luz principal esteja na posição do Sol, simulando a sua irradiação. Para isso utilizaremos o componente light na a-entity sol:
light="type: point; color: white; intensity: 2.5; castShadow: true"O A-Frame possui vários tipos de luz como ambient, directional, hemisphere, point, spot e probe, mas nenhuma delas corresponde a uma fonte de luz extensa para simular melhor a iluminação solar. Ainda assim, o tipo point, em que a luz é emitida igualmente em todas as direções a partir de um ponto, reproduz os efeitos astronômicos que queremos explorar. Utilizamos o atributo castShadow: true pois, por padrão, para poupar processamento, o A-Frame não renderiza sombras entre as entidades da cena.
É interessante também substituirmos a iluminação padrão da a-scene por uma luz ambiente fraca para obtermos um bom contraste entre a face dos astros iluminada pelo Sol e a face escura. Para isso, utilizaremos o tipo de luz ambient em uma nova a-entity logo no início da a-scene:
<a-entity>
light="type: ambient; color: white; intensity: 0.005"
</a-entity>Essa luz iluminará igualmente todos os objetos sem produzir sombras entre eles. Repare na diferença de intensidade (intensity) entre as duas luzes de forma a produzir o contraste desejado. De fato, essa luz ambiente praticamente não existe nos astros reais, mas uma pequena iluminação na face escura da Terra e da Lua facilita a percepção dos fenômenos.
Precisamos também informar que as duas entidades, a-entity terra e a-entity lua, precisam ser configuradas para receber e produzir sombras com o componente shadow:
shadow="receive: true; cast: true"Por fim, iremos definir a propriedade roughness (rugosidade) dos materiais da Terra e da Lua para o valor máximo de 1 (o padrão é 0,5):
material="src: #mapa_terra; roughness: 1"Essa propriedade define o quão difusa é a reflexão na superfície do material. Um roughness baixo produz um efeito espelhado e um valor alto um efeito fosco.
3.8 Elementos gráficos de referência
O nosso projeto STL está praticamente completo. Temos os movimentos de rotação e translação, as inclinações do eixo de rotação da Terra e do plano da órbita da Lua e a iluminação que reproduz a luz solar.
Embora esses elementos já sejam suficientes para trabalharmos os conceitos básicos de astronomia, podemos incluir elementos gráficos auxiliares que facilitam a percepção dos fenômenos. São eles:
- Uma seta ao longo do eixo de rotação terrestre
- Um plano para a órbita da Terra
- Um plano para a órbita da Lua
- Um mapa de fundo do céu noturno
3.8.1 Seta do eixo de rotação terrestre
Implementaremos a seta indicativa do eixo de rotação terrestre usando as geometrias cylinder e cone em uma nova entidade a-entity eixo_terra, a qual será inserida dentro da a-entity terra, da seguinte forma:
<a-entity id="eixo_terra">
<a-entity
geometry="primitive: cylinder; height: 0.60; radius: 0.007"
material="color: blue"
></a-entity>
<a-entity
geometry="primitive: cone; radiusBottom: 0.03; radiusTop: 0; height: 0.1; segmentsRadial: 4; segmentsHeight: 4"
material="color: blue"
position="0 0.30 0"
></a-entity>
</a-entity>3.8.2 Planos orbitais
Faremos os planos orbitais com a geometria circle.
O plano orbital da Terra é estático e ficará ao lado das entidades a-entity terra e a-entity lua:
<a-entity
id="plano_terra"
geometry="primitive: circle; radius: 2"
material="side: double; opacity: 0.1; emissiveIntensity: 20; emissive: blue"
rotation="90 0 0"
></a-entity>O plano orbital da Lua ficará dentro da a-entity inc_orb_lua pois terá que seguir essa inclinação:
<a-entity
id="plano_lua"
geometry="primitive: circle; radius: 0.5"
material="side: double; opacity: 0.1; emissiveIntensity: 20; emissive: white"
rotation="90 0 0"
></a-entity>Utilizamos o atributo opacity para que os planos sejam transparentes e não interfiram significativamente na visualização. Os atributos emissiveIntensity foram usados com valores altos para que os planos produzam uma luz própria e não sejam afetados pela luz solar atrapalhando a visualização.
3.8.3 Mapa do céu noturno
Para dar mais realismo, vamos inserir um mapa do céu noturno. O procedimento é semelhante aos mapas das superfícies dos astros, exceto que existe uma entidade específica para isso no A-Frame, chamada de a-sky. O mapa também precisa ser uma projeção cilíndrica equidistante (equirectangular). Vamos incluí-la dentro de uma a-entity que roda o mapa do céu de 23,4° de forma que os polos celestes da imagem coincidam com os polos celestes de rotação da Terra:
<a-entity rotation="23.4 0 0">
<a-sky src="#skymap"></a-sky>
</a-entity>Sendo que a imagem skymap utilizada deve ser incluída em assets da mesma forma que os demais mapas dos astros:
<img id="skymap" src="https://i.postimg.cc/9mjwfS4J/Tycho-Skymap-16384x08192.jpg"/>Essa imagem (Figura 3.3) foi obtida do catálogo estelar Tycho e colocada temporariamente no postimg para que pudesse ser carregada online pelo a-Frame.

3.9 Resultado final
<!DOCTYPE html>
<html>
<head>
<script src="https://aframe.io/releases/1.6.0/aframe.min.js"></script>
<script src="https://unpkg.com/aframe-orbit-controls@1.3.2/dist/aframe-orbit-controls.min.js"></script>
</head>
<body>
<a-scene>
<a-entity
camera
look-controls="enabled: false"
orbit-controls="target: 0 0 0; minDistance: 0; maxDistance: 180; initialPosition: 0 3 5; rotateSpeed: 1.5"
></a-entity>
<a-assets>
<img
id="mapa_sol"
src="https://upload.wikimedia.org/wikipedia/commons/thumb/9/99/Map_of_the_full_sun.jpg/1280px-Map_of_the_full_sun.jpg"
/>
<img
id="mapa_terra"
src="https://upload.wikimedia.org/wikipedia/commons/thumb/2/23/Blue_Marble_2002.png/1280px-Blue_Marble_2002.png"
/>
<img
id="mapa_lua"
src="https://upload.wikimedia.org/wikipedia/commons/thumb/d/d1/Solarsystemscope_texture_8k_moon.jpg/1280px-Solarsystemscope_texture_8k_moon.jpg"
/>
<img
id="skymap"
src="https://i.postimg.cc/9mjwfS4J/Tycho-Skymap-16384x08192.jpg"
/>
</a-assets>
<a-entity
light="type: ambient; color: #ffffff; intensity: 0.005"
></a-entity>
<a-entity rotation="23.4 0 0">
<a-sky src="#skymap"></a-sky>
</a-entity>
<a-entity id="pos_sol" position="0 1.2 0">
<a-entity
id="sol"
geometry="primitive: sphere; radius: 0.2"
material="src: #mapa_sol; emissiveIntensity: 0.5; emissive: #f7e927"
animation="property: rotation; to: 0 360 0; loop: true; dur: 50000; easing: linear"
light="type: point; color: white; intensity: 2.5; castShadow:true"
>
</a-entity>
<a-entity
id="plano_terra"
geometry="primitive: circle; radius: 2.3"
material="side: double; opacity: 0.1; emissiveIntensity: 20; emissive: blue"
rotation="90 0 0"
></a-entity>
<a-entity
id="orb_terra"
animation="property: rotation; to: 0 360 0; loop: true; dur: 30000; easing: linear"
>
<a-entity id="pos_terra" position="1.5 0.0 0">
<a-entity
id="rev_terra"
animation="property: rotation; to: 0 360 0; loop: true; dur: 30000; easing: linear; dir: reverse"
>
<a-entity id="inc_terra" rotation="23.4 0 0">
<a-entity
id="terra"
geometry="primitive: sphere; radius: 0.15"
material="src: #mapa_terra; roughness: 1"
animation="property: rotation; to: 0 360 0; loop: true; dur: 1000; easing: linear"
shadow="receive: true; cast: true"
>
<a-entity id="eixo_terra">
<a-entity
geometry="primitive: cylinder; height: 0.60; radius: 0.007"
material="color: blue"
></a-entity>
<a-entity
geometry="primitive: cone; radiusBottom: 0.03; radiusTop: 0; height: 0.1; segmentsRadial: 4; segmentsHeight: 4"
material="color: blue"
position="0 0.30 0"
></a-entity>
</a-entity>
</a-entity>
</a-entity>
<a-entity id="inc_orb_lua" rotation="-25 0 0">
<a-entity
id="plano_lua"
geometry="primitive: circle; radius: 0.8"
material="side: double; opacity: 0.1; emissiveIntensity: 20; emissive: white"
rotation="90 0 0"
></a-entity>
<a-entity
id="orb_lua"
animation="property: rotation; to: 0 360 0; loop: true; dur: 3000; easing: linear"
>
<a-entity id="pos_lua" position="0 0.0 0.8">
<a-entity
id="lua"
grabbable
geometry="primitive: sphere; radius: 0.05"
material="src: #mapa_lua; roughness: 1"
rotation="0 90 0"
shadow="receive: true; cast: true"
>
</a-entity>
</a-entity>
</a-entity>
</a-entity>
</a-entity>
</a-entity>
</a-entity>
</a-entity>
</a-scene>
</body>
</html>Veja também o sistema STL completo rodando no Glitch.
3.10 Aprimoramentos
Vamos aprimorar nosso projeto de forma a incluir diversidade de visualizações e interatividade.
3.10.1 Com os pés no chão
Até agora não mexemos na posição da câmera. Ela permaneceu fixa em uma a-entity a parte, fora do sistema de coordenadas do Sol. Mas podemos colocar a câmera onde quisermos, inclusive fixa na superfície da Terra de forma a reproduzir nossa visão do céu. Para isso, basta retirarmos a câmera original e colocarmos uma nova dentro da a-entity terra:
<a-entity
id="terra"
geometry="primitive: sphere; radius: 1.5; segmentsWidth:180; segmentsHeight:360"
material="src: #mapa_terra; roughness: 1"
animation="property: rotation; to: 0 360 0; loop: true; dur: 10000; easing: linear"
shadow="receive: true; cast: true"
>
<a-entity camera look-controls position="1.35 0.755 0" fov="80"></a-entity>
</a-entity>No código acima, aumentamos a segmentação da esfera terrestre para uma superfície mais suave e aumentamos o seu raio para um horizonte menos curvo. Fora isso, o código é essencialmente o mesmo do Código 3.8.
Essa posição da câmera produz a visualização mostrada no Vídeo 3.8.
Veja também o sistema Sol-Terra-Lua com câmera fixa na superfície da Terra no Glitch.
3.10.2 Interação com os objetos
No A-Frame é muito simples incluir interação com as mãos do usuário. Basta incluir o componente hand-tracking-grab-controls em uma a-entity para cada mão:
<a-entity id="leftHand"
hand-tracking-grab-controls="hand: left;"
></a-entity>
<a-entity id="rightHand"
hand-tracking-grab-controls="hand: right;"
></a-entity>E incluir o componente grabbable nos objetos que poderão ser agarrados com as mãos. Por exemplo, para que a Terra seja “agarrável” incluímos o componente grabbable dentro da a-entity correspondente:
<a-entity id="terra"
grabbable
geometry="primitive: sphere; radius: 0.15"
material="src: #mapa_terra; roughness: 1"
position="1 1.2 0"
shadow="receive: true; cast: true"
></a-entity>O Código 3.9 corresponde a um sistema STL alternativo mais simples em que os astros não são animados, mas apenas habilitados para serem “agarráveis” pelo usuário. Apesar dessa simplicidade, as condições de iluminação dentro desse ambiente virtual são difíceis de reproduzir em um ambiente real, possibilitando explorar com riqueza os fenômenos que mencionamos anteriormente envolvendo as fases da Lua, eclipses e estações do ano. Vide Vídeo 3.9.
<!DOCTYPE html>
<html>
<head>
<script src="https://aframe.io/releases/1.6.0/aframe.min.js"></script>
</head>
<body>
<a-scene>
<a-assets>
<img id="mapa_sol"
src="https://upload.wikimedia.org/wikipedia/commons/thumb/9/99/Map_of_the_full_sun.jpg/1280px-Map_of_the_full_sun.jpg"
/>
<img id="mapa_terra"
src="https://upload.wikimedia.org/wikipedia/commons/thumb/2/23/Blue_Marble_2002.png/1280px-Blue_Marble_2002.png"
/>
<img id="mapa_lua"
src="https://upload.wikimedia.org/wikipedia/commons/thumb/d/d1/Solarsystemscope_texture_8k_moon.jpg/1280px-Solarsystemscope_texture_8k_moon.jpg"
/>
<img id="skymap"
src="https://i.postimg.cc/9mjwfS4J/Tycho-Skymap-16384x08192.jpg"
/>
</a-assets>
<a-entity camera look-controls position="0.5 1.6 0.3"></a-entity>
<a-entity id="leftHand"
hand-tracking-grab-controls="hand: left;"
></a-entity>
<a-entity id="rightHand"
hand-tracking-grab-controls="hand: right;"
></a-entity>
<a-entity
light="type: ambient; color: #ffffff; intensity: 0.005"
></a-entity>
<a-sky src="#skymap"></a-sky>
<a-entity id="sol"
grabbable
geometry="primitive: sphere; radius: 0.1"
material="src: #mapa_sol; emissiveIntensity: 0.5; emissive: #f7e927"
light="type: point; color: white; intensity: 2.5; castShadow:true"
position="0 1.2 0"
>
</a-entity>
<a-entity id="terra"
grabbable
geometry="primitive: sphere; radius: 0.15"
material="src: #mapa_terra; roughness: 1"
position="0.75 1.2 0"
shadow="receive: true; cast: true"
></a-entity>
<a-entity id="lua"
grabbable
geometry="primitive: sphere; radius: 0.05"
material="src: #mapa_lua; roughness: 1"
rotation="0 90 0"
position="1 1.2 0.5"
shadow="receive: true; cast: true"
>
</a-entity>
</a-scene>
</body>
</html>Veja também o sistema Sol-Terra-Lua manipulável no Glitch.
3.10.3 Configurando a aplicação web para uso offline
Ter que depender de uma conexão com a internet toda vez que necessitar fazer uma atividade em Realidade Virtual pode ser limitante, principalmente quando não se dispuser de uma infraestrutura robusta de internet por WiFi, o que é muito comum no ambiente escolar.
Existe uma forma simples de resolver isso através do chamado service worker com cache estático. Ele é usado para interceptar as requisições e armazenar os recursos necessários no cache do navegador, permitindo que a página continue a funcionar mesmo sem conexão com a internet. É um caminho eficiente e moderno, especialmente quando se espera que os usuários usem a página offline.
Para isso, são necessários dois passos. Primeiramente, deve-se incluir o script Javascript (Código 3.10) dentro do elemento body do arquivo html principal.
<script>
if ('serviceWorker' in navigator) {
window.addEventListener('load', () => {
navigator.serviceWorker.register('/service-worker.js')
.then((registration) => {
console.log('Service Worker registrado com sucesso:', registration);
})
.catch((error) => {
console.log('Falha ao registrar o Service Worker:', error);
});
});
}
</script>body do arquivo html de forma a permitir que a aplicação continue acessível ao navegador mesmo estando offline.
Por fim, deve-se criar um arquivo como o nome service-worker.js na mesma pasta do arquivo html principal com o com o conteúdo do Código 3.11.
// service-worker.js
self.addEventListener('install', (event) => {
event.waitUntil(
caches.open('my-cache').then((cache) => {
return cache.addAll([
'/',
'/index.html',
'https://aframe.io/releases/1.6.0/aframe.min.js'
]);
})
);
});
self.addEventListener('fetch', (event) => {
event.respondWith(
caches.match(event.request).then((response) => {
return response || fetch(event.request);
})
);
});service-worker.js para acesso offline da aplicação web. Aqui estamos considerando que o arquivo principal chama-se index.html.
É recomendado que o service-worker seja habilitado somente quando o projeto estiver pronto. Na fase de desenvolvimento, que requer que a página seja recarregada várias vezes, pode haver o cache indesejado de versões antigas da página html, causando confusão. Para garantir que a versão mais atual da página seja carregada com o service-worker ativo é necessário limpar o cache do navegador.
3.11 Palavras finais
Com isso, concluímos este minicurso. Apesar do A-Frame permitir a programação usando exclusivamente linguagem HTML, é possível usar todo o poder da linguagem Javascript para desenvolver aplicações mais sofisticadas. O modo correto de fazer isso no A-Frame é através da criação de novos Components, os quais receberão toda a lógica de programação em Javascript. Além disso, o A-Frame disponibiliza acesso a todas as funcionalidades da poderosa biblioteca gráfica Three.js (pois é uma abstração desta). E existe também as componentes criadas pela comunidade de desenvolvedores, as quais abrangem uma boa diversidade de usos. Escolhemos não abordar essas possibilidades devido à curta duração deste minicurso.
Expressão cunhada pelo astrônomo e divulgador científico Carl Sagan ao descrever a imagem da Terra capturada pela sonda Voyager 1, a uma grande distância. No retrato, o planeta aparece como um minúsculo ponto azul. Sagan utilizou essa imagem para refletir sobre a humildade e a responsabilidade da humanidade em relação ao único lar conhecido.↩︎
Na verdade, a Lua não gira em tono da Terra, mas em torno do centro de massa do sistema Terra-Lua, assim como a própria Terra. Por motivos didáticos, usaremos o sistema de referência centrado na Terra para implementar o movimento orbital da Lua. Essa aproximação não é tão ruim, uma vez que o centro de massa do sistema está bem mais próximo da Terra do que da Lua.↩︎
A expressão em italiano que significa “E, no entanto, ela se move” teria sido dita por Galileu Galilei após ser forçado pela Inquisição a renegar sua defesa do heliocentrismo. Galileu teria murmurado a frase em desafio, reafirmando sua convicção, mesmo após a retratação oficial. Entretanto, não há evidências da vericidade dessa fala.↩︎
O movimento de precessão do eixo de rotação terrestre realmente existe e é conhecido como precessão dos equinócios. Mas é um movimento muito lento, em que uma precessão completa dura 26 mil anos e é causada pela interação gravitacional da Terra oblata principalmente com o Sol e a Lua.↩︎
Neste projeto, iremos considerar que a normal ao plano da órbita da Lua possui uma direção fixa no espaço. Mas isso não é verdade, pois assim como o eixo de rotação da Terra, o plano orbital da Lua possui um movimento de precessão (semelhante ao movimento de um bambolê) só que com um período bem mais curto de 18,6 anos. Apesar disso, representa uma alteração de direção em torno de 5% ao ano e não altera o fato de que temos dois momentos no ano em que ocorrem os eclipses separados por aproximadamente 6 meses. De um ano para o outro as datas dos eclipses vão se deslocando de 3 a 4 semanas devido a essa precessão. É esse movimento que determina o ciclo de Saros e sua causa se deve à força gravitacional diferencial que a Lua sofre do Sol ao longo da sua órbita em torno da Terra.↩︎